导数
最最基础
f(x)的导数f'(x)表示函数f(x)在x处的斜率
运算
函数&对应の导数
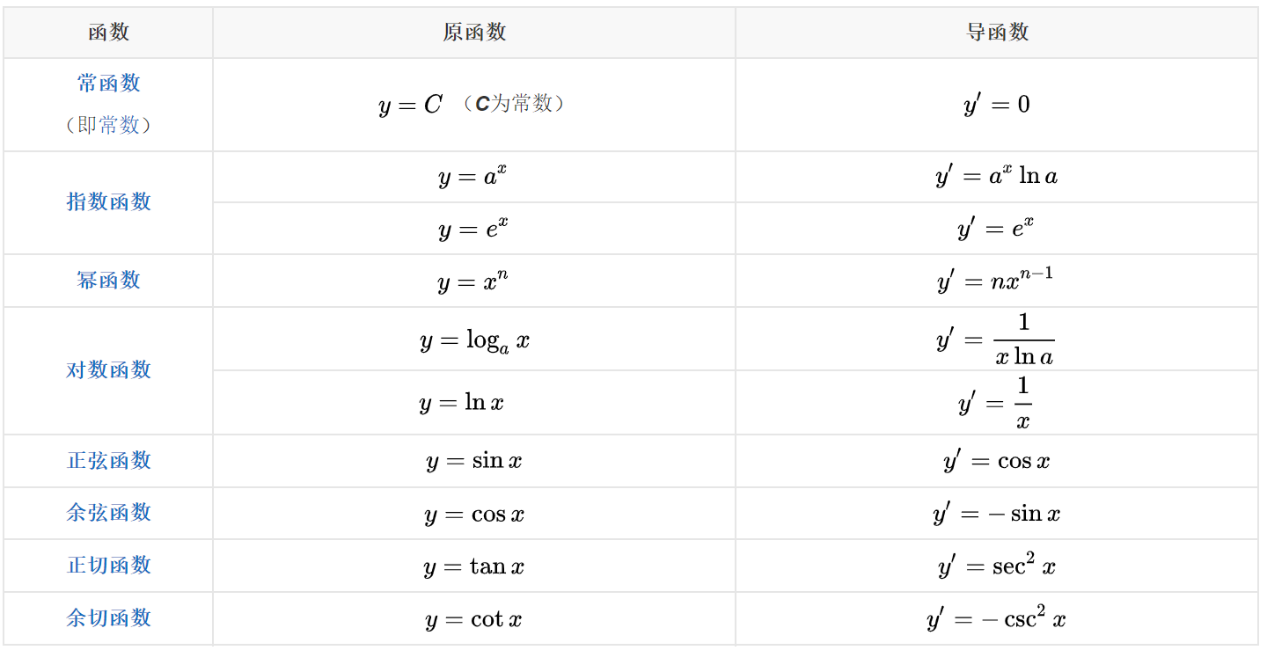
导数の四则运算
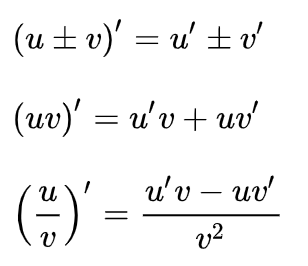
复合函数の导数
复合函数对自变量的导数,等于已知函数对中间变量的导数,乘以中间变量对自变量的导数
f[g(x)]′=f′[g(x)]g′(x)
六大基本函数图像
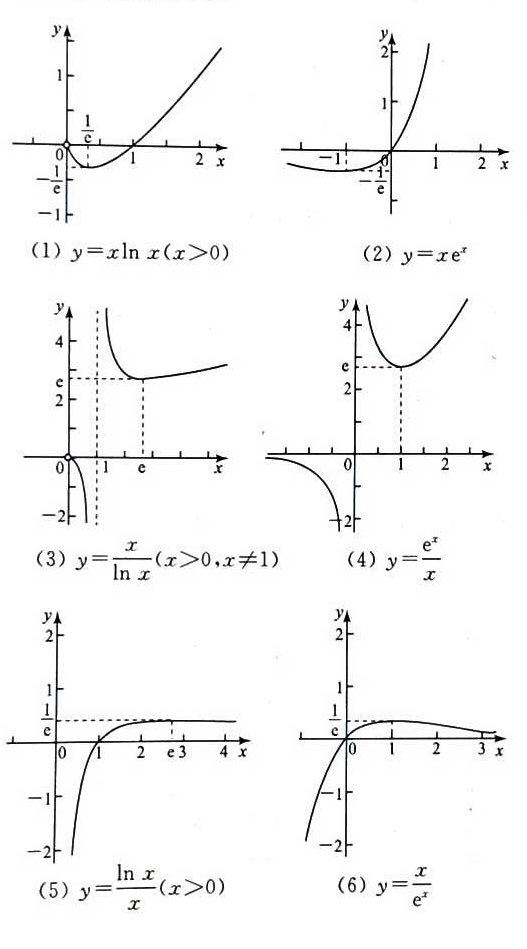
构造

例1 ↓

例2 ↓

洛必达法则

变形↓

同构式
同构式的操作,就是若希望证明一个不等式,那么通过一系列的
(简单但又不完全简单、难但又不完全难的)
变换,使式子两侧变为参数不同的相同函数,再根据函数图像的单调性,将问题转化为函数中参数的不等式
举个小栗子

同构的一些小技巧↓
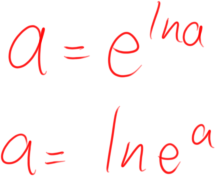
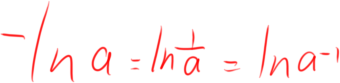
注意
1.同构式一般特别精妙,且最后两侧的参数不一定有共同之处(如次数不同),就像例子中的e^a和b
2.同构式需要六大函数图像作为支持


朗博_同构式的一种特殊变形
下面这个叫朗博的东西强的一批,建议看所有题目
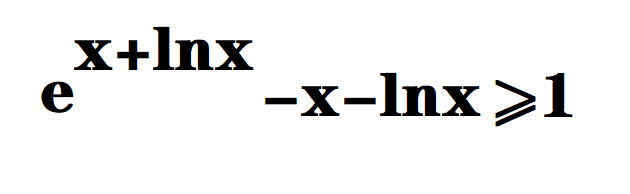

对数均值不等式
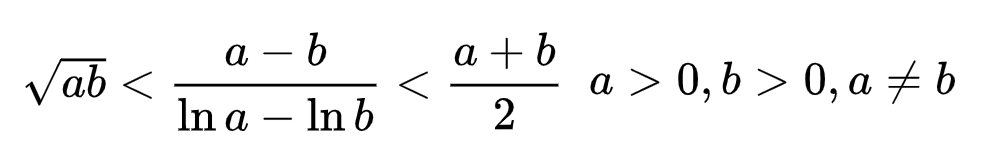
这个不等式很好用,就是考试时候需要当场表演证明

几个例题
例题1 ↓

例题2 ↓

精妙的小不等式*2
这俩不等式常用于放缩
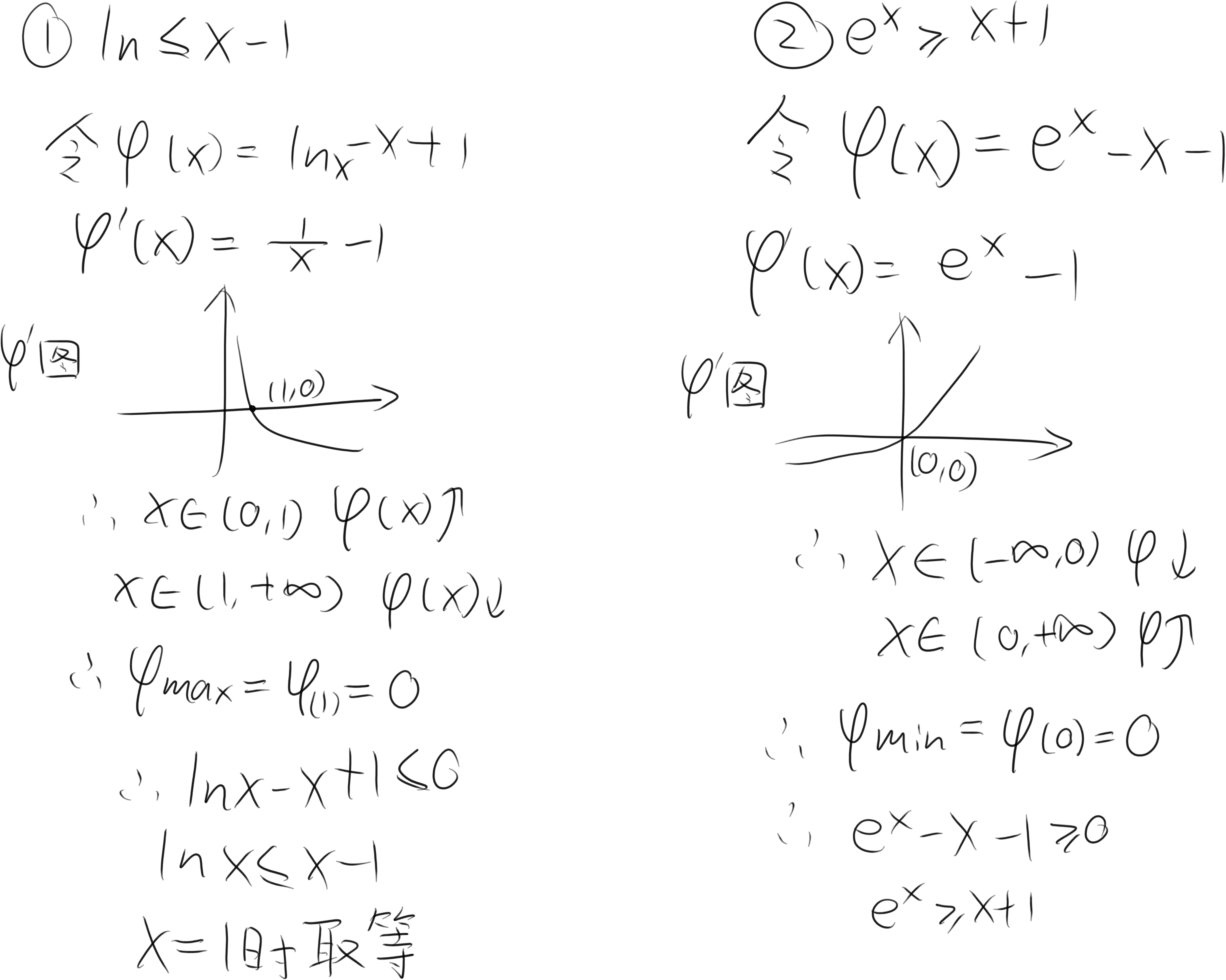
放缩
零点差类型题目
使用两切线夹零点(有个三明治定理仿佛类似),是放缩的一种
这种题的一般套路及策略↓
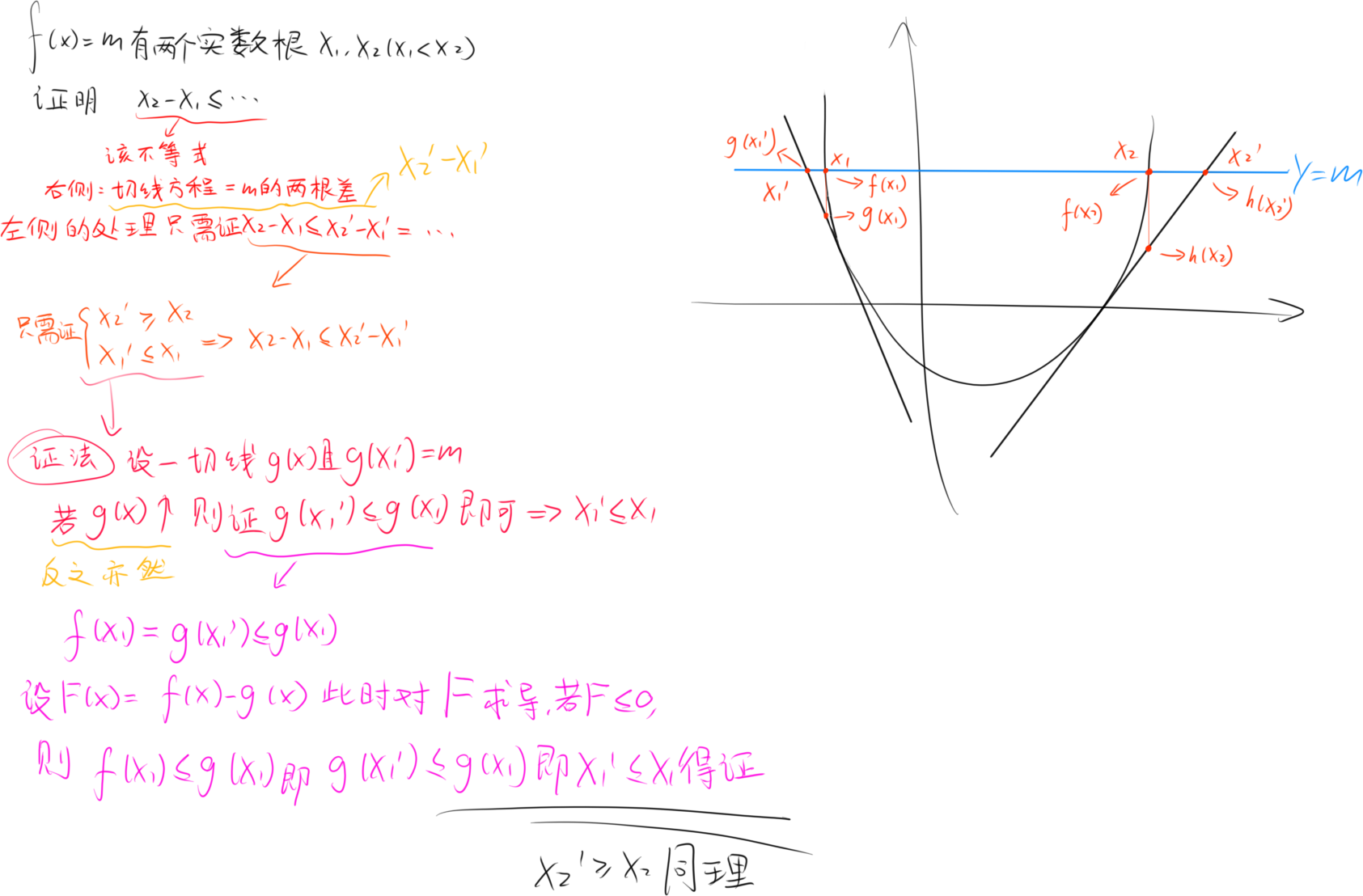
确定切线的方法
1.一般题目会送一个切点
2.另一个切点可根据右侧的式子用待定系数法推
3.可以试一试函数零点的切线
4.猜
例题1:这个题很巧两个切点是都零点


例题2:很悲伤的,题目给了一个另一个要算


例题3:两零点处切线


泰勒公式
极值点偏移

必要性探路
清君侧
处理对数用,嘎嘎强
http://lanqi.org/skills/18608/
不动点&稳定点
函数不动点,在数学中是指被这个函数映射到其自身的一个点,即函数f(x)的取值过程中,如果有f(x₀)=x₀,就称x₀为f(x₀)的一个不动点
对此定义可以从代数意义和几何意义去理解
(一)代数意义:若方程f(x₀)=x₀有实根x₀,则f(x₀)=x₀有不动点x₀
(二)几何意义:若函数y=f(x)与函数y=x有交点(x₀, y₀),则x₀为f(x)的不动点
同理,上面被称为一阶不动点,那么对应的就有二阶不动点,也叫稳定点
f(f(x₀))=x₀
说明:
1.稳定点是函数图像和他的反函数的交点的横坐标
2.若x₀为不动点,那么x₀为稳定点;但稳定点只有在函数单调递增是才等于不动点
Eg_1

Eg_2,看罢

Eg_3 和数列有点关系

隐零点
https://zhuanlan.zhihu.com/p/108156179