圆锥曲线：从入门到入门

焦点弦

对于左右圆锥曲线，焦点弦都满足

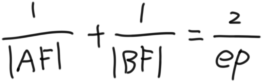
p是焦准距，准线到焦点的距离

e是离心率

抛物线设点

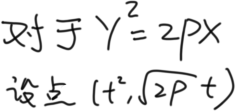
这样可以使一个点只有一个参数简化运算

圆锥曲线设线

1.恒过y轴上一点 y = kx + b

2.恒过x轴上一点 x = my + c

3.恒过x轴上一点且斜率已知存在 y = k ( x – x0 )

4.恒过一定点( x0 , y0 ) y – y0 = k ( x – x0 )

若出现( y1 – y0 )( y2 – y0 ) 或 ( x1 – x0 )( x2 – x0 ) 或 (y1 – yα
)( y2 – yα ) 或 ( x1 – xα )( x2 – xα
)，知而不用，正常设线即可（如下图

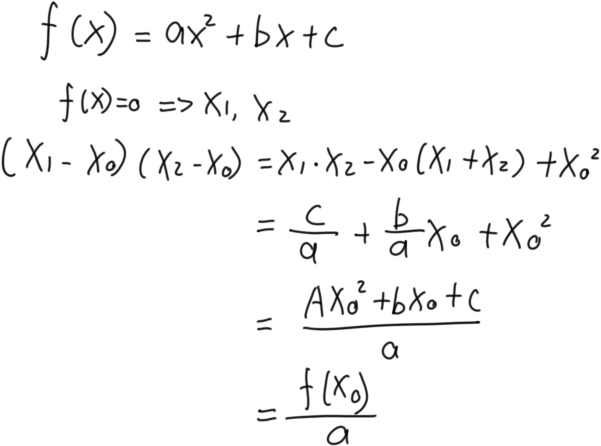
又如今年高考题

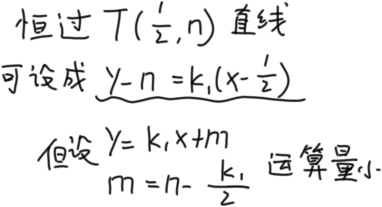
举一个小例子(手撕一下2021年高考题)

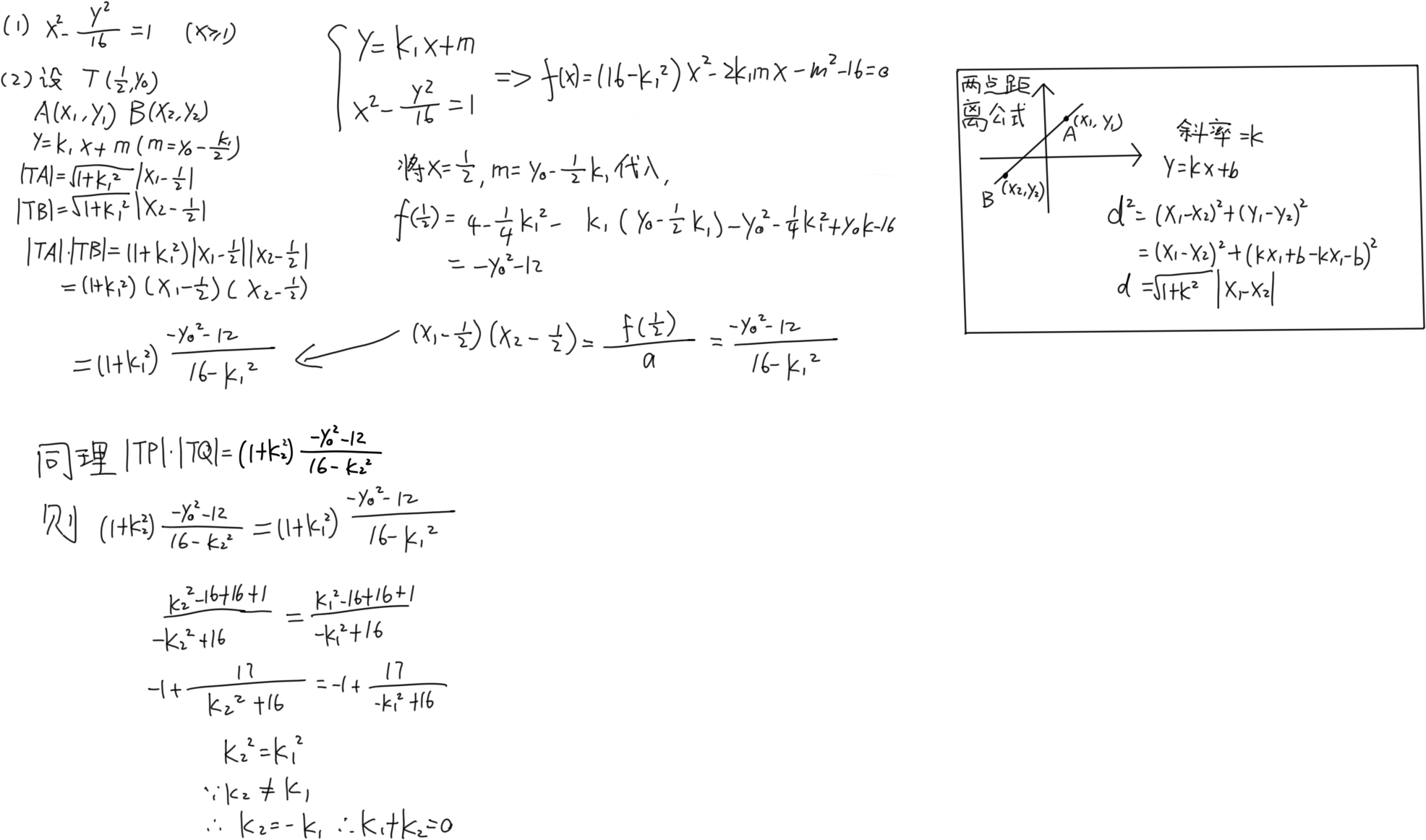
两点间距离公式

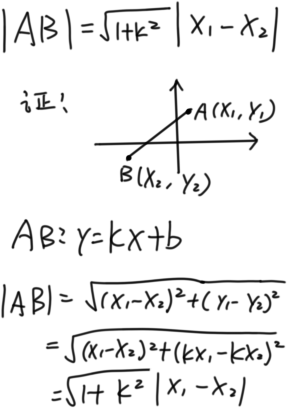
两点相切问题

下面有请第一位受害者出场

显然设点联立很难，所以

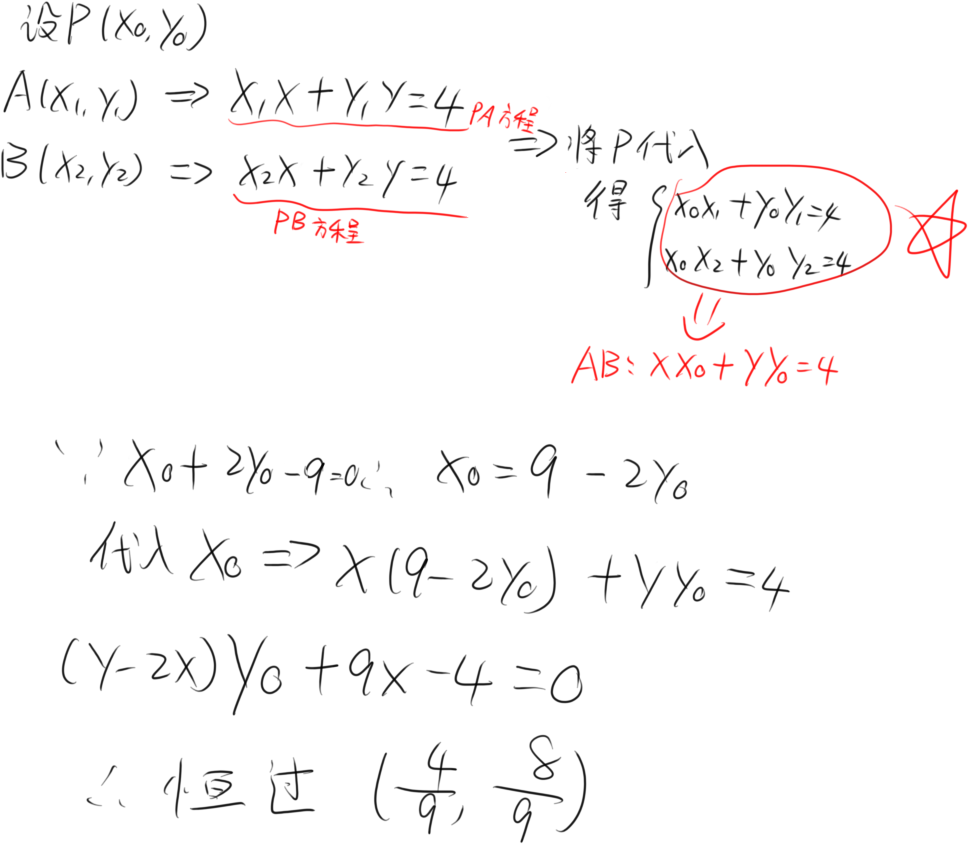
通过精妙的操作把AB直线用P坐标表示，再根据P的方程即可消到只剩一个参数

下面有请第二位受害者出场

依然常龟操作即可

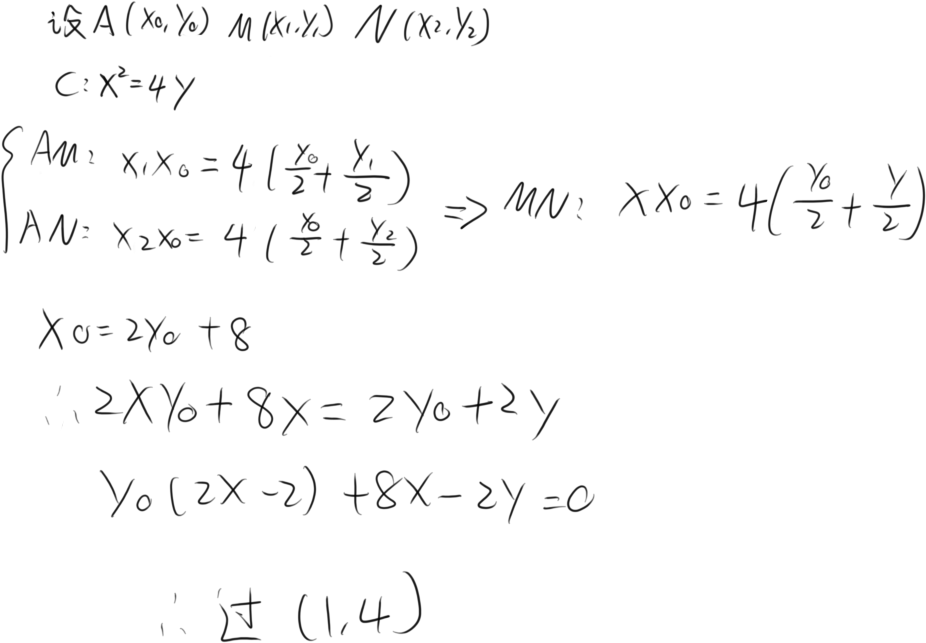
三jio函数设点(离谱

非对称的求解

有请受害者

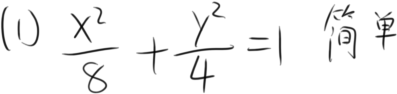
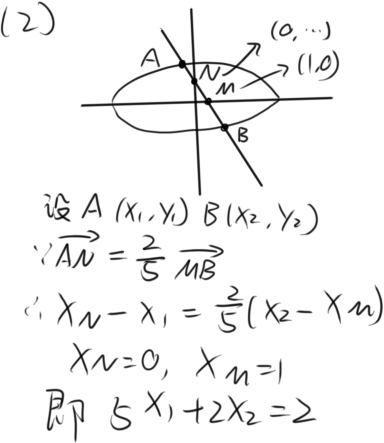
到了这步显然卡关了，因为正常操作都是带X₁+X₂，X₁和X₂系数相等，此时需要一个神奇的操作

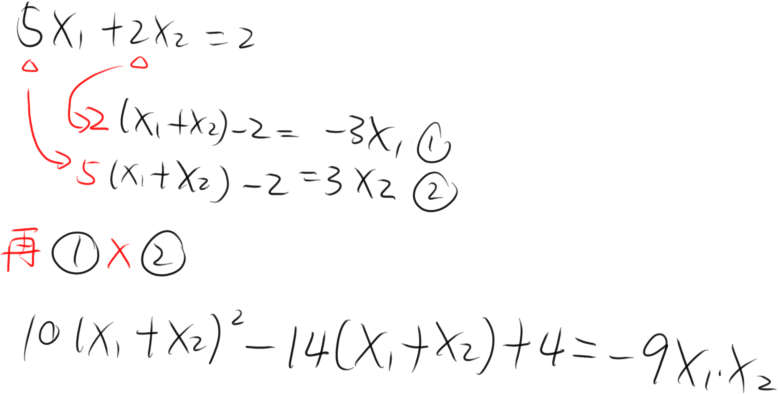
点差法&有心二次曲线的垂径定理

因为用点差法可以精妙地推出垂径定理，所以写在一块

有心二次曲线为椭圆，双曲线，圆

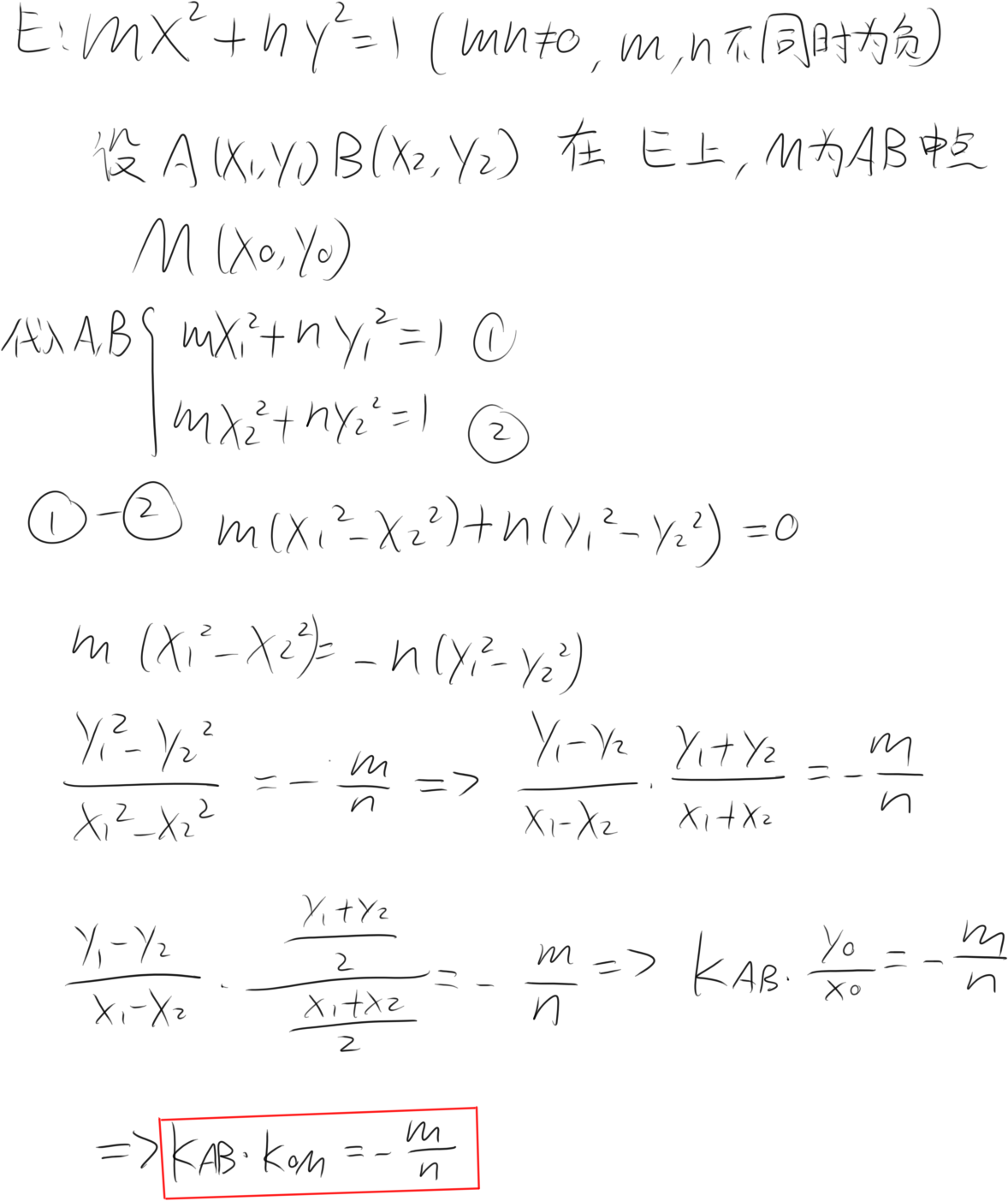
红框为有心二次曲线的垂径定理

涉及弦的中点可以用点差法

定比点差法

点我!

椭圆的仿射变换

压缩坐标轴使椭圆成为圆

焦点三角形

斯特瓦尔特定理

调和点列