椭圆入门
椭圆
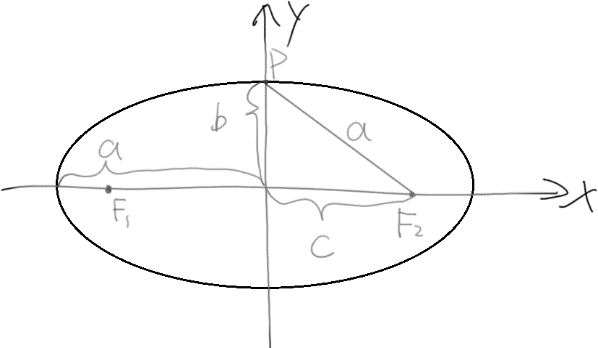
施法前摇
a:半长轴
b:半短轴
F1F2:焦距
c:焦距/2
根据勾股定理得知a²=b²+c²
第一定义
到平面内两个定点F1与F2的距离的和为一个常数(大于|F1F2|)的所有点的轨迹为椭圆
设M点的坐标为(x,y) , 椭圆P=
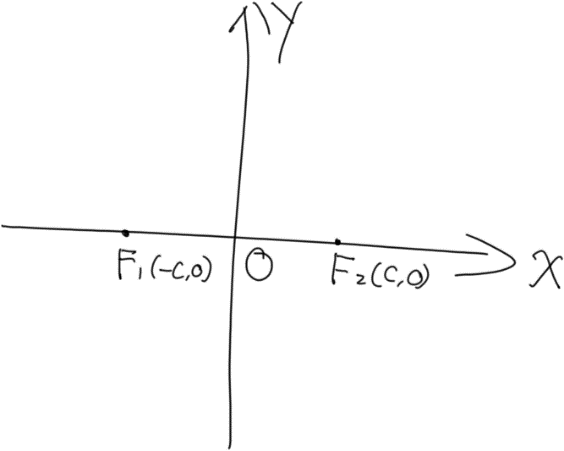
标准方程(焦点在x轴
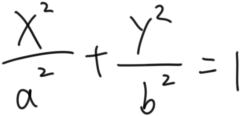
推导过程如下,已知
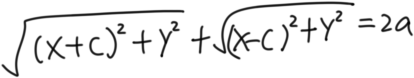
思路一:分子有理化
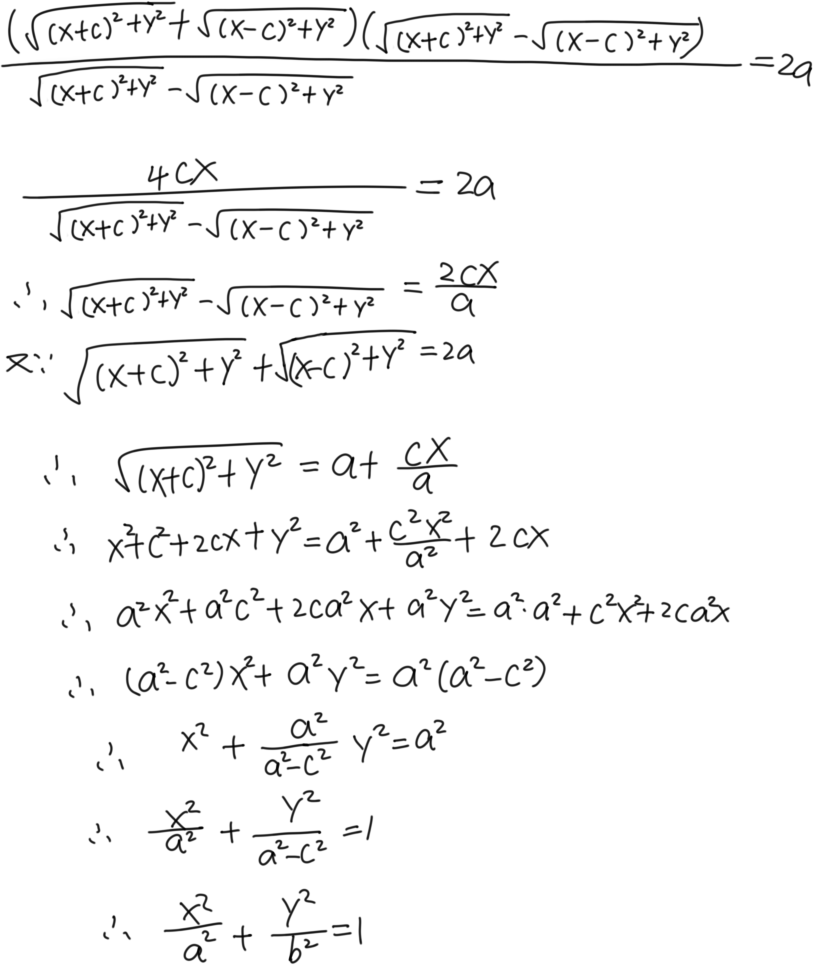
好耶!wuhu take off!
思路二:移项
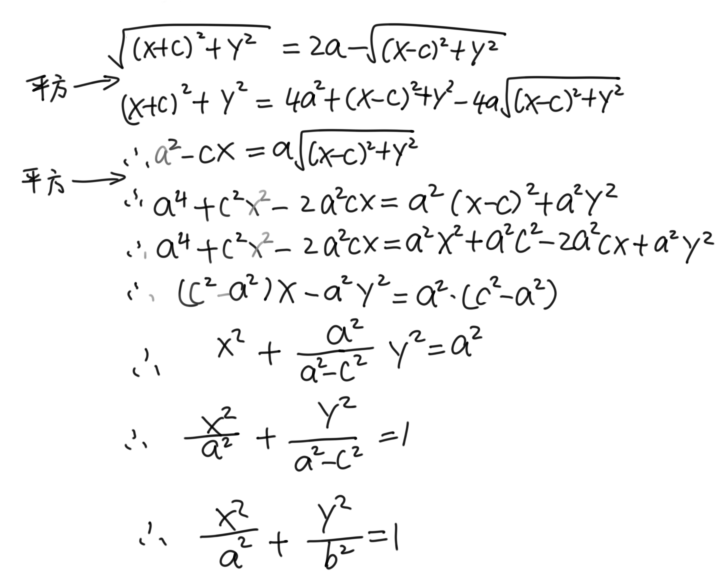
这就是智慧(bu
第二定义
平面内一点到定点的距离与到定直线距离的比值是个常数e(0<e<1)
一些解释
1. 定点为焦点F1,F2
2. 定直线为对应的准线 x=a²/c与x=-a²/c
3. 离心率e=c/a
推导
在第一定义移项的推导中,已经知道
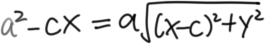
(已经在往回翻了
那么
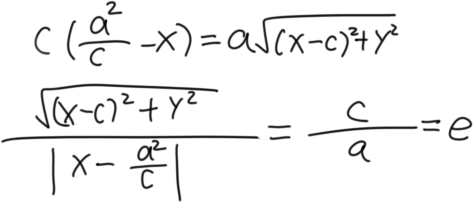
焦半径
椭圆上任意一点P与焦点连线的线段为焦半径
设P(x0,y0)为椭圆上一点,那么焦半径为|PF1|,|PF2|,且|PF1|=a+ex0,|PF2|=a-ex0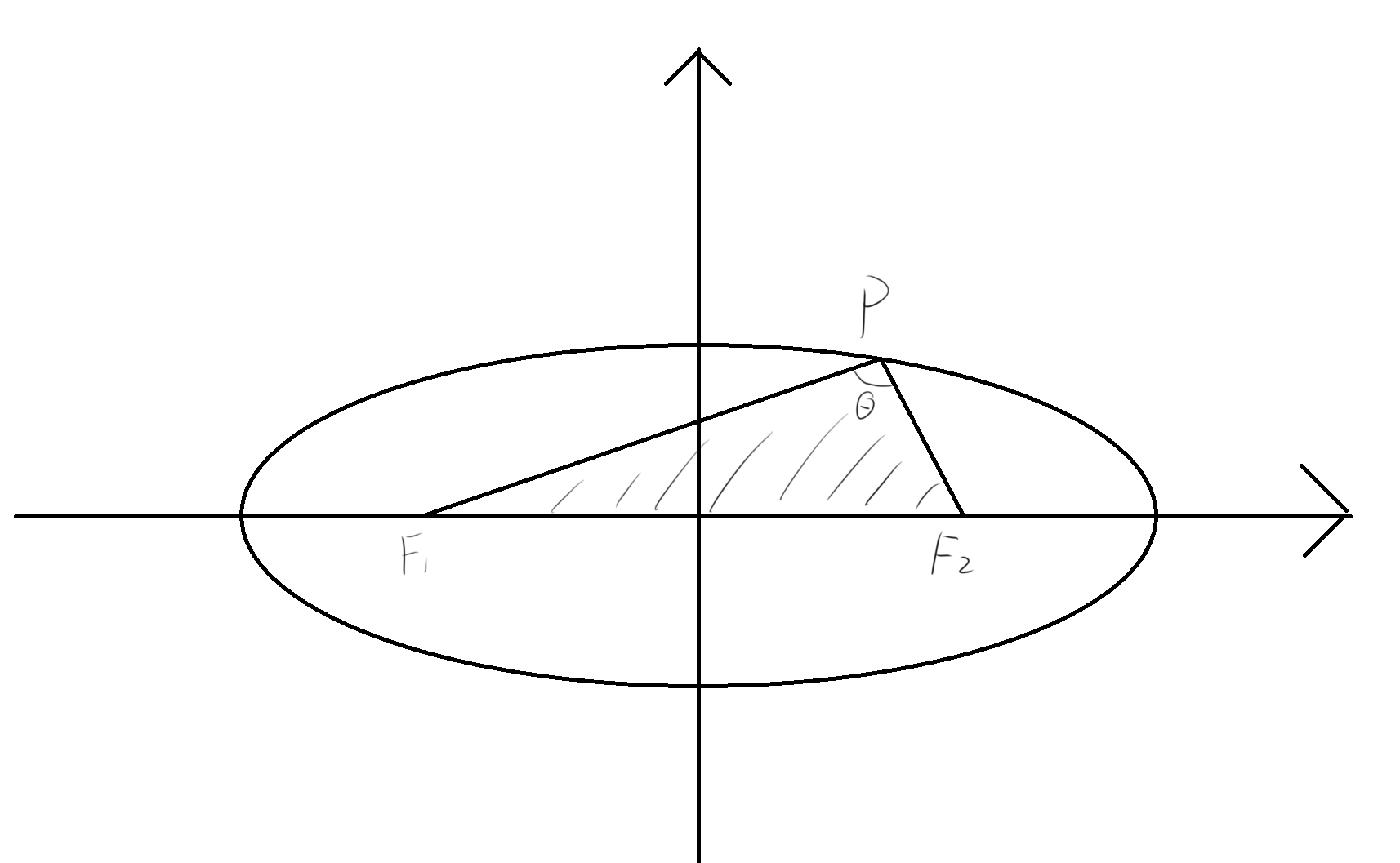
推导
思路一:第二定义
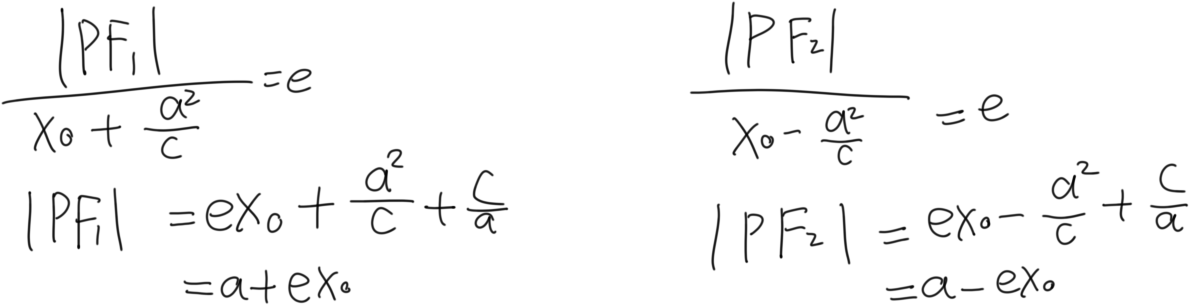
思路二:第一定义
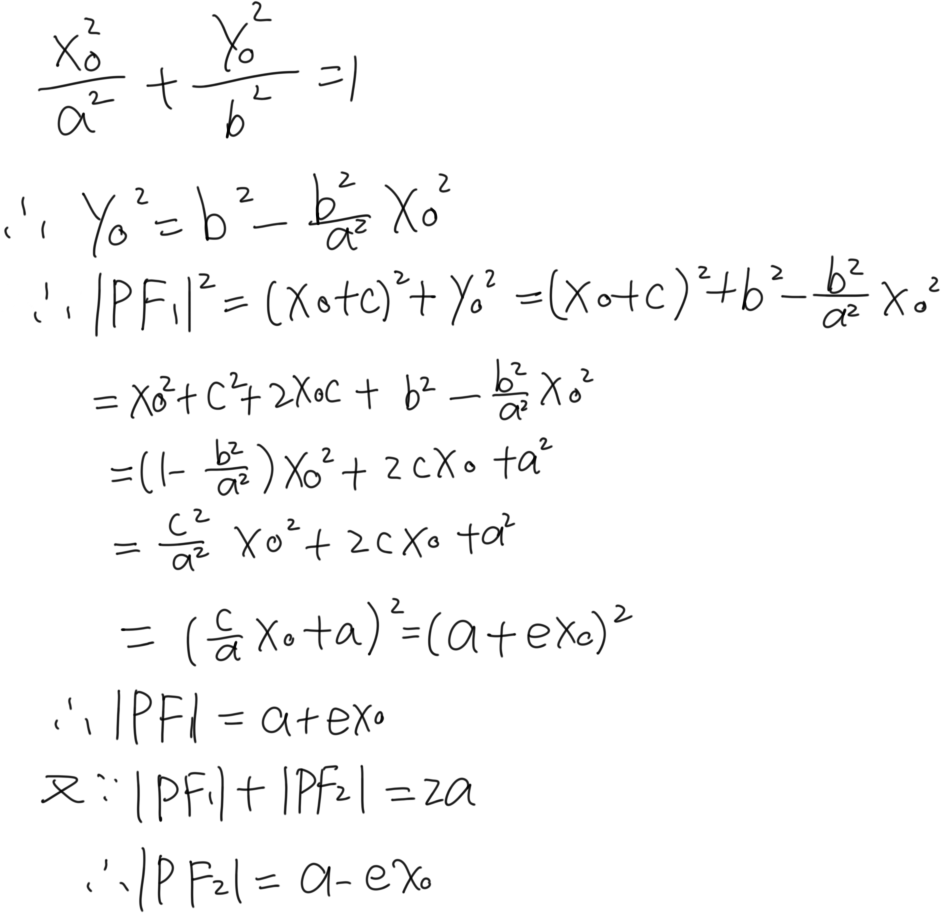
注意①
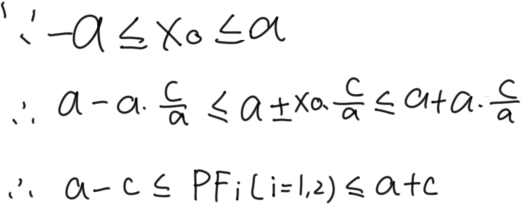
注意②
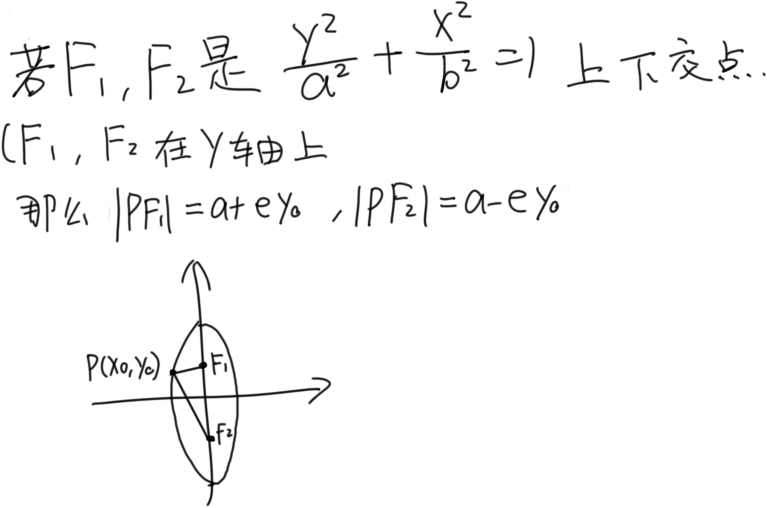
焦半径(倾斜角式
首先引入焦准距的概念,焦准距p=a²/c-c=b²/c,也就是准线到焦点的距离
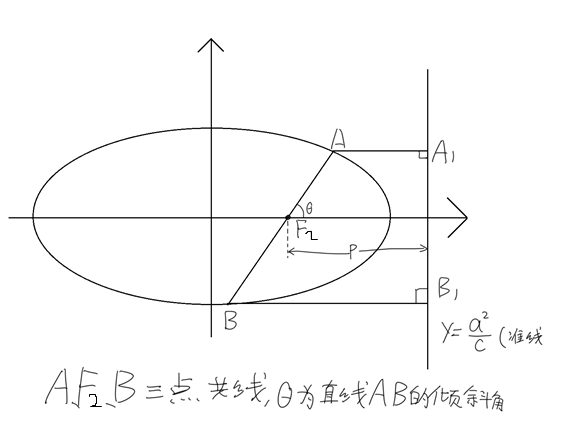 看这精妙的图,然后就有如下操作
看这精妙的图,然后就有如下操作
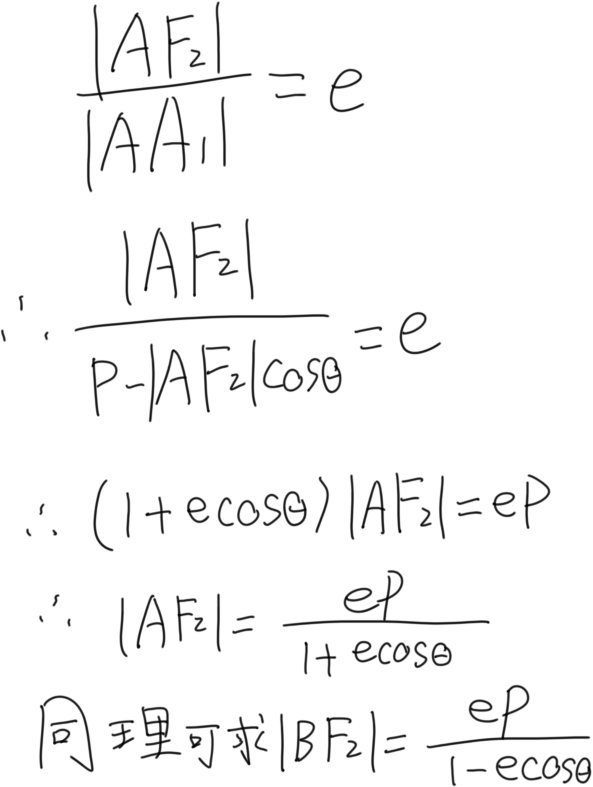 这个骚操作之后又能求出|AB|
这个骚操作之后又能求出|AB|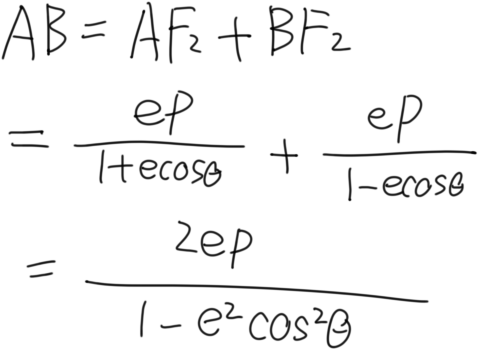
此时故事往两个方向发展
方向①
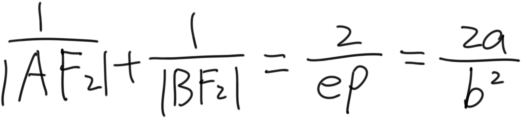 (是个感觉能用上的式子
(是个感觉能用上的式子
方向② 当AB⊥x轴时, 倾斜角=0°,cos=0,此时|AB| = 2ep = 2 * c/a * b²/c
= 2 b²/a
此时线段AB也称为通径
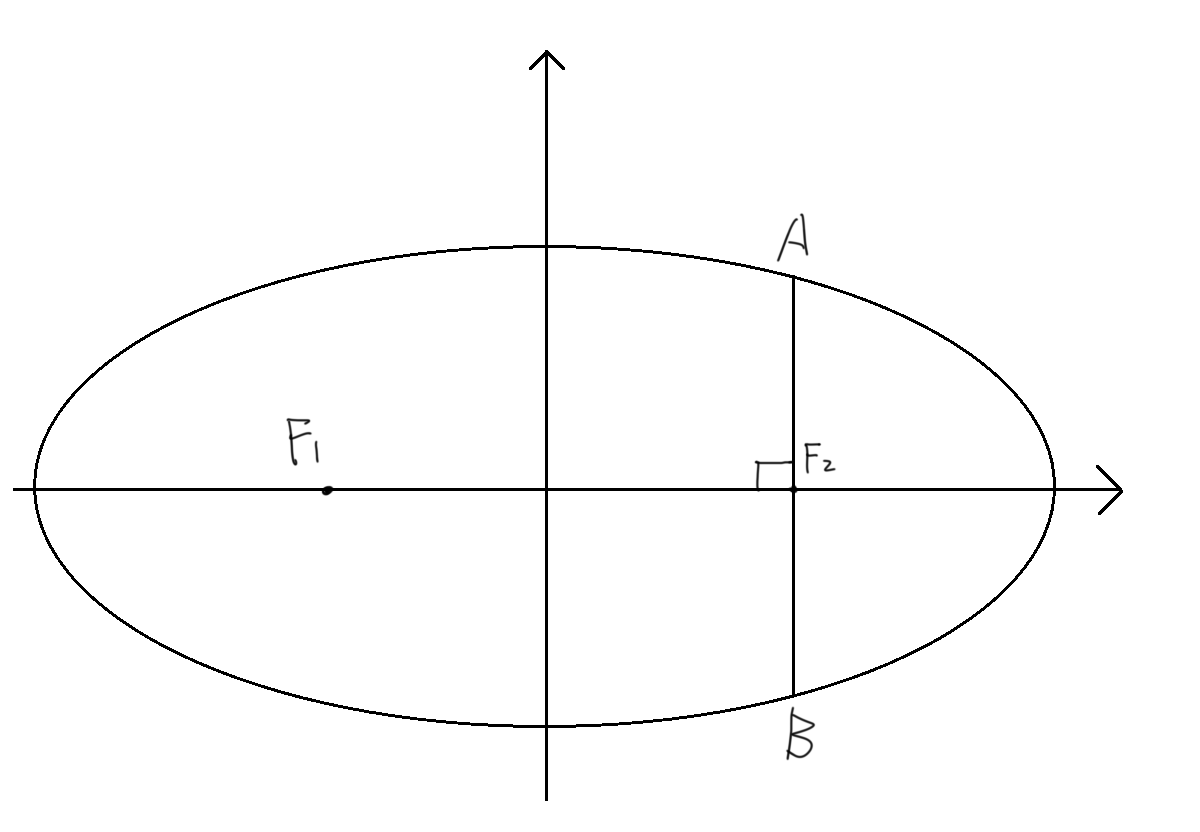
关于把焦点和椭圆上一点P连起来发生了奇怪的现象这档事

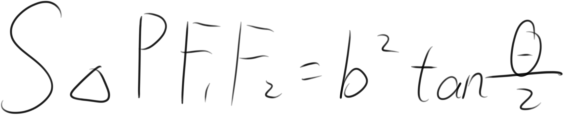
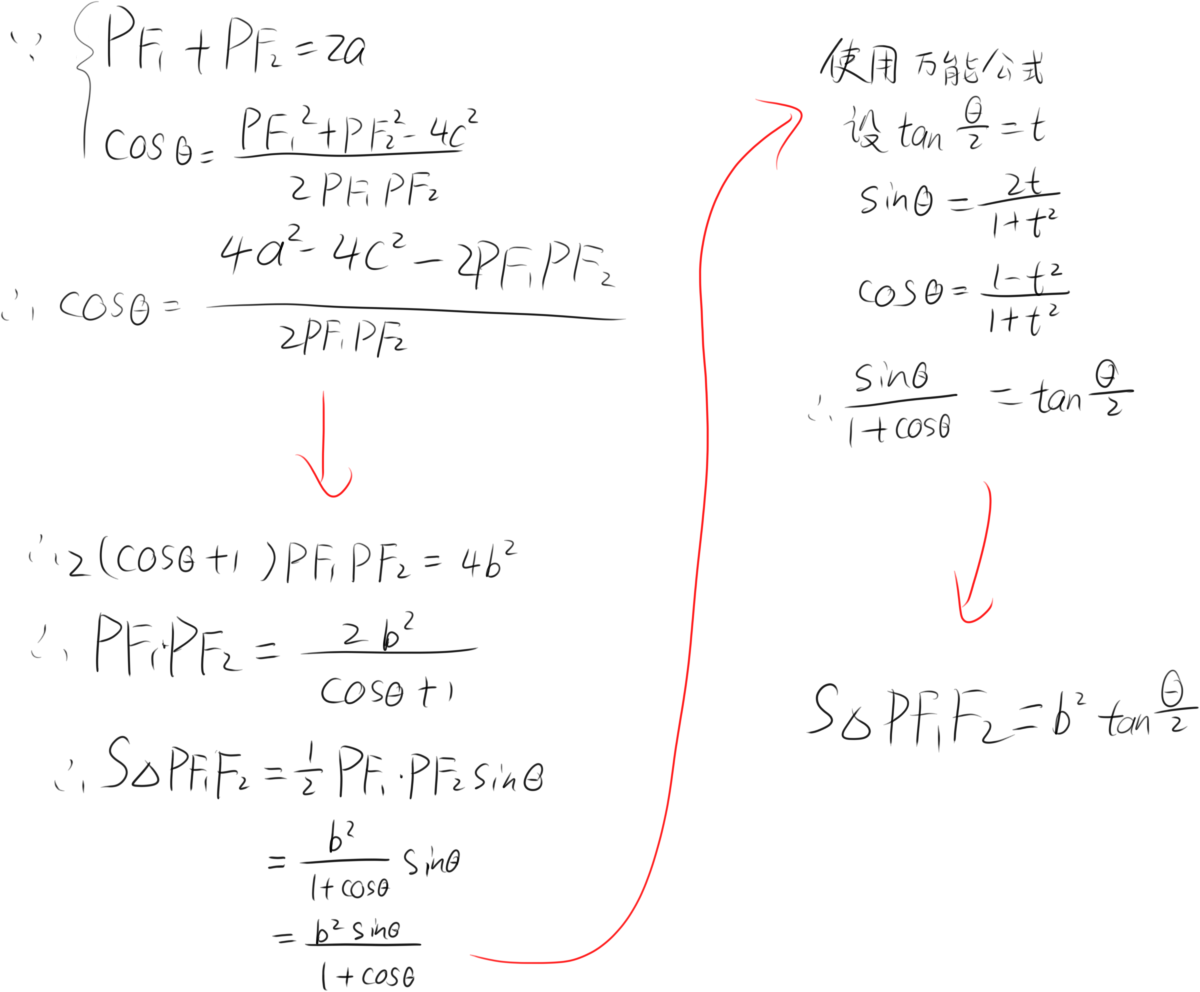
推导
第三定义
平面内与两定点连线的斜率之积为常数(除-1外)的点的轨迹称为椭圆(不包括两定点)
说明:两定点并不是焦点,是椭圆交于X轴的两点(a,0)与(-a,0)
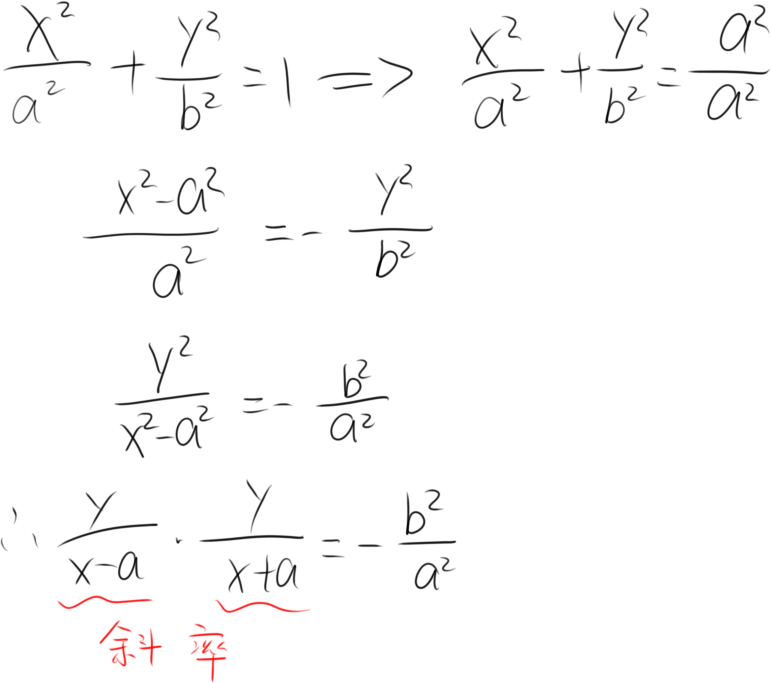
关于斜率的说明
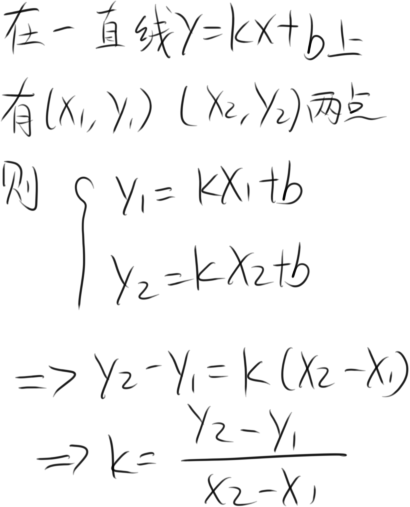
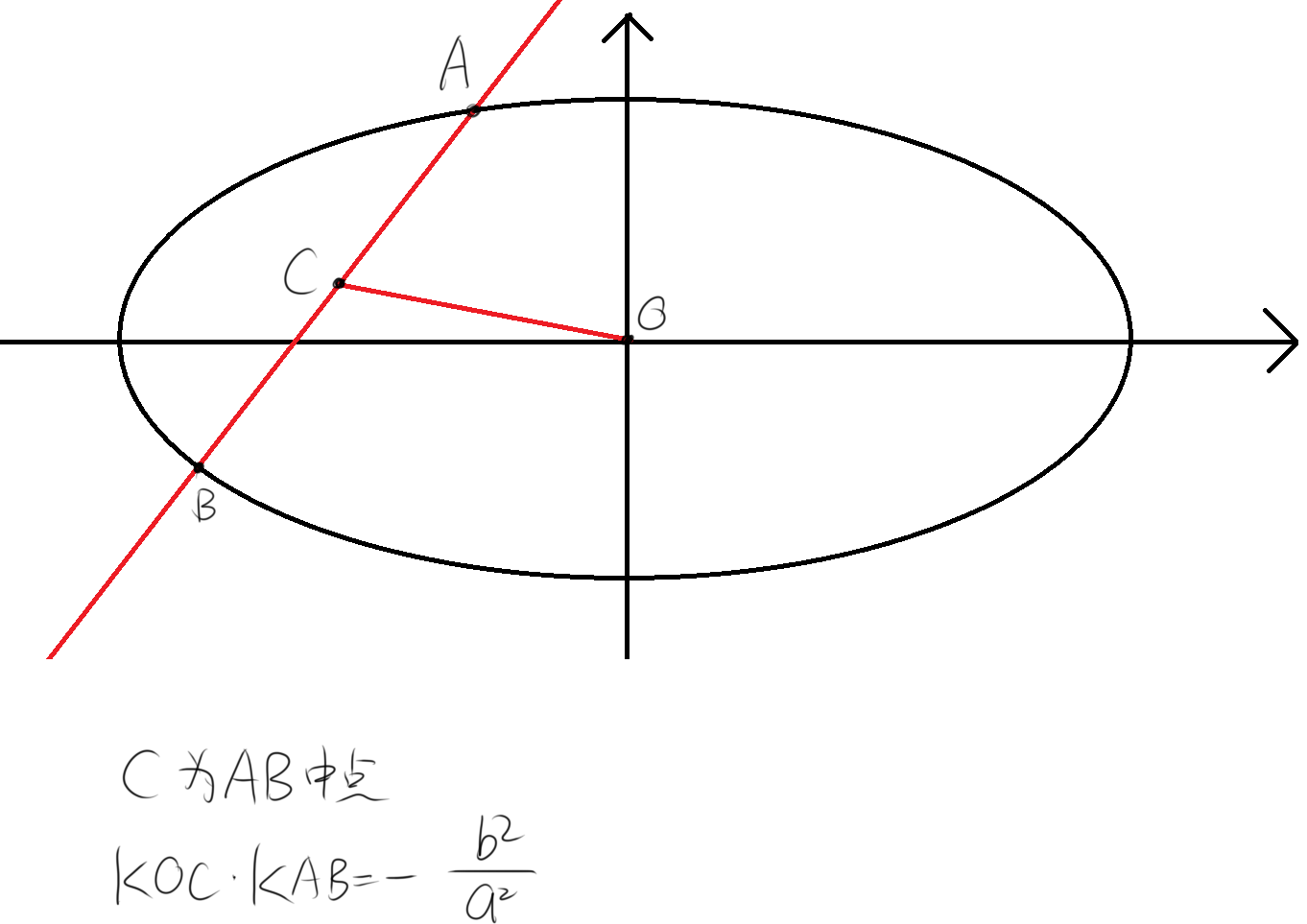
椭圆中的垂径定理
先说是啥
推导
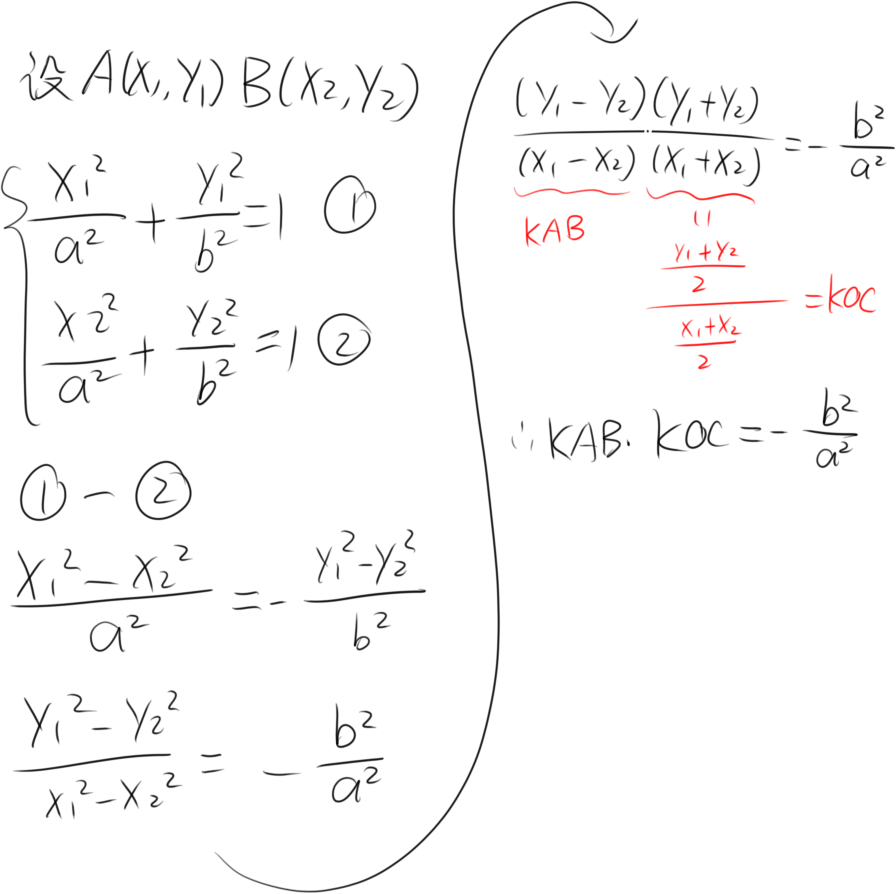
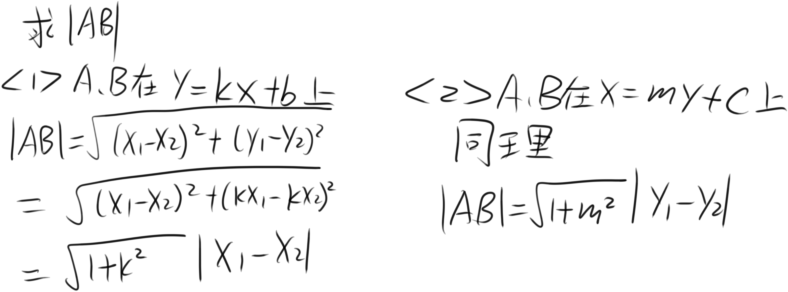
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.